Erläuterungen zu diesem Arbeitsblatt

pdf-Datei

Dieses Arbeitsblatt wurde gemeinsam mit Studierenden des WBK AG Viersen in asynchroner Kommunikation bearbeitet, d.h. in einem Kursforum wurde das Original von der Lehrkraft eingestellt und dann von den Studierenden zu Hause am PC bearbeitet. Die Fragen und Kommentare der Studierenden und der Lehrkraft befinden sich in den durch ????? gekennzeichneten Feldern.

Von der Ableitung an einer Stelle x_o zur Ableitungsfunktion

Bekanntes:

Steigung von Geraden (2-Punkte-Form, Steigungsdreieck)

Steigung von Sekanten (2 Punkte auf dem Funktionsgraphen von f)

Steigung von Tangenten (Annäherung des einen Punktes auf dem Graphen an den Punkt (x_o;f(x_o))

è Steigung einer Funktion f an einer Stelle x_o

è f’(x_o) =

?????????????????????

AK: Wo liegt der Unterschied zwischen der Steigung einer Sekante und der Steigung einer Tangente ?

SE: Steigung einer Sekante hat zwei feste Punkte auf dem Graphen. Tangente hat nur einen Punkt auf dem Graphen.

MO: Eine Tangente ist eine spez. Sekante deren Abstand zwischen P0 und P1 unendlich klein ist. Die Tangente hat einen Grenzwert.

Gds: zum letzten Satz (er ist so nicht richtig): Berechnung der Steigung von Sekanten ist bekannt, aber die Berechnung der Steigung einer Tangente, die den Funktionsgraphen in einem Punkt berührt, ist nicht möglich. Daher wählt man die Hilfskonstruktion, dass man die Steigung von Sekanten berechnet, die immer näher an dem Tangentenberührpunkt liegen, also einen unendlich kleinen Abstand voneinander haben. Um dies mathematisch ausdrücken zu können, wählt man den Grenzwert der Steigung dieser Sekanten und definiert dies als Steigung der Tangente.

?????????????????????

Neues

Da wir den Punkt (x_o; f(x_o)) beliebig, aber fest gewählt haben, können wir mit Hilfe des obigen Differenzenquotienten die Steigung der Funktion f an jeder beliebigen Stelle berechnen. Wir erhalten dann wieder eine Funktion, nämlich die Ableitungsfunktion f’, die die Steigung der zugehörigen Funktion f an jeder Stelle angibt. Da wir es gewohnt sind, die Variable mit x zu bezeichnen, schreiben wir f(x) und f’(x).

(Ist die Verwirrung jetzt komplett? Hoffentlich nicht!

Vielleicht hilft folgendes Beispiel, bzw. das Durcharbeiten

der Seiten 54-55 im Buch L-S)

??????????????????????

AK: Warum muss man für die Ableitungsfunktion den Grenzwert bestimmen?

MO: Vielleicht hängt das damit zusammen, dass man bei einer gegeben Funktion f nicht für jede Stelle x0 erneut den Differenzquotienten und seinen Grenzwert bestimmen muss. Die Funktion f`: x ® 2x liefert für jede Stelle x0 die Ableitung f`(x0).

Ob das so Richtig ist, keine Ahnung!!!

Gds: Richtig, per Definition ist die Ableitung (Steigung) der Grenzwert des Differenzenquotienten an einer Stelle xo. Wenn ich diese Stelle wieder als eine Variable x auffasse, erhalte ich eine Funktion, nämlich die Ableitungsfunktion f’ von f.

???????????????????????????

Bsp: f(x) = x²

Gesucht: Steigung an den Stellen 1; 3; 4; 5; -3; -7

f’(x_o) = = = (x+x_o) = 2x_o 

_{??????????????}

_{AK:Wie kommt man auf das Ergebnis 2x0?}

_{SE: Weil man auch x0+x0 schreiben könnte????}

MO: sehe ich genau so

????????????????????

f’(1) = 2

f’(3) = 6

f’(4) = 8

f’(5) = 10

f’(-3) = -6

f’(-7) = -14

Zeichen Sie die Funktionsgraphen von f und f’.

Da das Rechnen mit dem Differenzenquotienten sehr umständlich ist, wollen wir uns zunächst auf das zeichnerische Differenzieren, d.h. das Ermitteln der Ableitungs- oder Steigungsfunktion von f konzentrieren. Dazu zeichnen wir an den Graphen von f in ausgewählten Punkten die Tangenten. Der Wert der Steigung der Tangenten an diesen Punkten ist dann der Funktions- oder y-Wert der Ableitungsfunktion f’.

Bsp:

f(x) = x²

Tangenten an den Stellen 0; 1; 3; 4; 5; -3; -7

Zeichen Sie den Funktionsgraphen von f und die Tangenten an den obigen Stellen in ein Koordinatensystem und ermitteln Sie die Steigung der Tangenten mit Hilfe von Steigungsdreiecken.

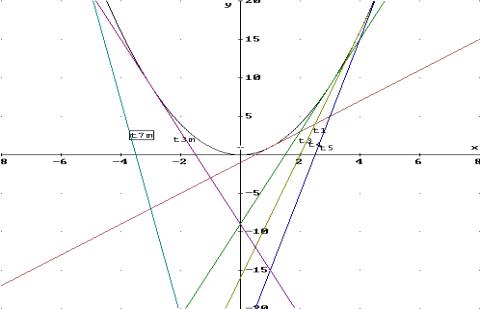
Die abgelesenen Werte der Steigung der Tangenten an den ausgewählten Stellen tragen wir in ein weiteres Koordinatensystem ein.

???????????????

AK: Wie ist das gemeint?

Gds: zu jedem x auf der x-Achse gibt es einen Punkt auf dem Graphen von f, in dem eine Tangente gezeichnet werden kann. Die Steigung dieser Tangente kann mit Hilfe des Steigungsdreiecks ermittelt werden. Dies ergibt den y-Wert der Ableitungsfunktion f’, die in ein neues Koordinatensystem eingetragen werden kann.

????????????

An der Stelle 0 hat die Funktion f die Steigung 0, also ist f’(0) = 0, d.h. der Punkt (0;0) kann eingezeichnet werden.

An der Stelle 1 hat die Funktion f die Steigung 2, also ist f’(1) = 2, d.h. der Punkt (1;2) gehört zum Funktionsgraphen von f’.

Ebenso gehören die Punkte (3;6), (4;8), (5;10), (-3;-6) und (-7;-14) zum Funktionsgraphen von f’.

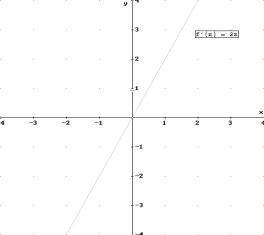
Es zeigt sich, dass die Ableitungs- oder Steigungsfunktion f’ zu f mit f(x) = x² die Funktionsgleichung f’(x) = 2x hat. (Wen wundert’s?!)

Das zeichnerische Differenzieren ist ein ungenaues Verfahren, hilft aber, wesentliche Zusammenhänge zwischen Funktionen und ihren Ableitungs-, bzw. Steigungsfunktionen zu erkennen.

Jetzt kommen die beiden Arbeitsblätter zum Tragen, die ich Ihnen in der letzten Stunde gegeben habe. Skizzieren Sie den Verlauf der Ableitungsfunktionen. Weitere Übungen finden Sie im Internet: mathe-online Ableitungspuzzle. Es kommt dabei nicht auf exaktes Zeichnen, bzw. Bestimmen der Funktionswerte von f’ an, sondern auf das Erkennen des allgemeinen Verlaufs der Graphen. Alles klar??!

NEE

Gds: Schade, mal sehen, ob die letzten Klarheiten im Präsenzunterricht beseitigt werden können ;))